編按：不管是學業還是運動，都有許多人汲汲營營想拚第一名，考進台大或進入奧運殿堂。能力固然重要，但《長勝》作者指出「個人能力的矛盾」，也就是能力愈強，運氣對考試、比賽結果的影響力就愈大。為什麼？
雙罐模型
想像你有兩個裝滿球的罐子。每顆球上面都有一個號碼，就像樂透彩一樣。其中一個罐子的球代表個人能力，另一個罐子的球則代表運氣。數字越大越好。你從一個罐子拿出一顆代表能力的球、再從另一個罐子拿出一顆代表運氣的球，然後把兩個號碼加起來得到一個數字（見圖表3-2）。
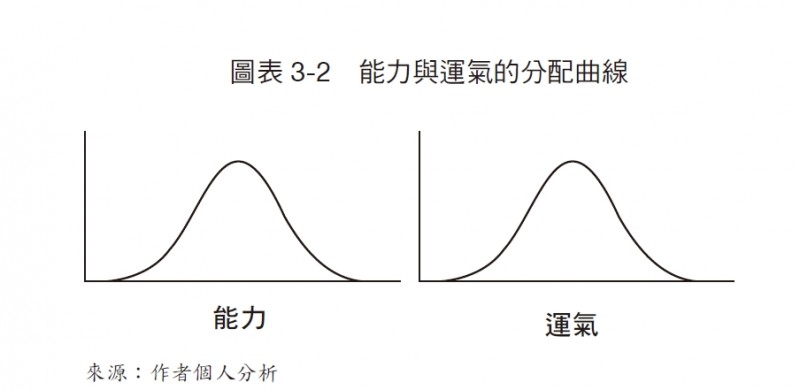
如果要表達一個完全仰賴個人能力的活動，我們可以把運氣罐子裡的球全部換上0。如此一來，只有代表個人能力的球才會被計入。如果我們要一個完全靠運氣的活動（例如輪盤），我們就把另一個罐子的球全部換成0。
然而，事實上大多數的活動其實都混雜了能力與運氣。
我們可以用一個簡單的例子來說明。假設代表能力的罐子裡只有三個號碼：–3、0 和3；代表運氣的罐子則有–4、0 和4。我們很快可以列出所有可能性：–7 代表著能力最差、運氣不佳；7 則是結合了卓越能力與好運氣（見圖表3-3）。當然，我們想要分析的真實狀況遠比這個例子複雜許多，但這些數字已經足以說明幾個重點。
因此，就算能力很強，但如果運氣的影響夠大，且從罐子中拿求的次數很少的話，還是有可能得到很低的分數。舉例來說，如果你的能力有3 分、但你從運氣罐抽到了–4，那麼運氣的影響便超過了能力，你便得到–1。你也可能完全沒有能力卻得到好結果。你的能力低到只有–3，但運氣卻有4，加起來分數仍然是1，結果不算差。
當然，隨著你增加樣本數量，這種效果也跟著消退。你可以這樣想：假設你的能力指數一直穩定維持在3 分。你只從運氣的罐子抽籤。短期來看，你可能會抽到一些代表好運氣或壞運氣的數字，這種效應可能會維持一段時間。不過把時間拉長的話，你抽出的運氣號碼期望值將是0，因為球的號碼是0、4和–4，剛好平均為0。最後，你的能力，也就是0，終究會顯現出來。 （相關報導： 為何許多年輕人畢業後搶著考公職？他不解「沒配股、分紅」根本落後一生，過來人曝最大優勢 ｜ 更多文章 ）
能力越強，運氣越重要
這個概念同樣適用於我所謂的「個人能力的矛盾」。隨著個人能力持續提升，個人表現會變得比較穩定，因此運氣就變得更重要。哈佛大學知名古生物學家史蒂芬．傑伊．古爾德（Stephen Jay Gould）用這個概念來解釋，為何自泰德．威廉斯（Ted Williams）1941年在大聯盟紅襪隊創下整季0.406的打擊率記錄後，再也沒有球員的打擊率可以維持在四成以上。古爾德先提到幾個常見的解釋。首先，夜間比賽、長途舟車勞頓、人才流失、投手變強，都使得打者受到壓抑。儘管這些因素或許都有一些影響，但都不足以解釋為何無法達到四成打擊率。另一個可能是，威廉斯不僅是那個年代最強的打者，甚至比之後至今的球員都還要強。古爾德馬上否定這個說法，因為證據顯示，只要是能夠用數字測量的運動，球員的長期表現都會逐漸進步。威廉斯當年固然是非常優秀的球員，但放在今天的大聯盟，恐怕也很難如此大放異彩。
